OPTIMIZACIÓN 1

En matemáticas la optimización o programación matemática intenta dar respuesta a un tipo general de problemas donde se desea elegir el mejor entre un conjunto de elementos. En su forma más simple, el problema equivale a resolver una ecuación de este tipo:

Donde x = (x₁,...,x_n) es un vector y representa variables de decisión, f(x) es llamada función objetivo y representa o mide la calidad de las decisiones (usualmente números enteros o reales) y Ω es el conjunto de puntos o decisiones factibles o restricciones del problema.

Algunas veces es posible expresar el conjunto de restricciones Ω como solución de un sistema de igualdades o desigualdades.

Un problema de optimización trata entonces de tomar una decisión óptima para maximizar (ganancias, velocidad, eficiencia, etc.) o minimizar un criterio determinado (costos, tiempo, riesgo, error, etc). Las restricciones significan que no cualquier decisión es posible.

EJEMPLO

El beneficio neto mensual, en millones de euros, de una empresa que fabrica autobuses viene dado por la función:

B(x)= 1.2x − (0.1x)³

donde x es el número de autobuses fabricados en un mes.

1. Calcula la producción mensual que hacen máximo el beneficio.

2. El beneficio máximo correspondiente a dicha producción.

optimización 2

De todos los triángulos isósceles de 12 m de perímetro, hallar los lados del que tome área máxima.

La función que tenemos que maximizar es el área del triángulo:

Relacionamos las variables:

2x + 2y = 12

x = 6 − y

Sustituimos en la función:

Derivamos, igualamos a cero y calculamos las raíces.

Realizamos la 2ª derivada y sustituimos por 2, ya que la solución y = 0 la descartamos porque no hay un triángulo cuyo lado sea cero.

Por lo que queda probado que en y = 2 hay un máximo.

La base (2y) mide 4m y los lados oblicuos (x) también miden 4 m, por lo que el triangulo de área máxima sería un triangulo equilatero.

OPTIMISACION

punto de inflexion

7) Puntos de inflexión.

    Un punto se llama de inflexión si en él la función cambia el sentido de la concavidad, por tanto en los puntos de inflexión la segunda derivada tiene que cambiar de signo y por tanto en él la segunda derivada tiene que ser cero.

Para determinar los puntos de inflexión hay dos métodos:

    A) Se determinan los intervalos de concavidad, si en uno de esos intervalos la función es cóncava hacia arriba o hacia abajo y en el siguiente cambia el sentido de la concavidad, siendo el extremo del intervalo un punto del dominio de definición en el que la función es continua, tendremos un punto de inflexión.

Si nos fijamos en el ejemplo que aparece en la determinación de los intervalos de concavidad se tiene que en (a,f(a)) y en (d,f(d)) hay puntos de inflexión.

B) Teorema 7.-

Sea a un punto del dominio de definición tal que f''(a)=0 y que f'''(a)…0, entonces la función tiene en (a,f(a)) un punto de inflexión.

Dem.

Si f'''(a)<0, tiene que existir un intervalo centrado en a en el que x (a-x ,a+x ) se verifique que f'''(x)<0, por tanto en ese intervalo, aplicando el teorema 2 se tiene que f'' es decreciente. Como f''(a)=0 entonces x (a-x ,a) f''(x)>0 (puesto que x<a) y por tanto f es cóncava hacia arriba; si x (a,a+x ) se tiene que x>a y como f''(a)=0 y f'' decreciente entonces f''(x)<0 y por tanto f es cóncava hacia abajo. Uniendo los dos resultados anteriores se tiene que f cambia en a de concavidad y por tanto tiene en a un punto de inflexión.

El caso f'''(a)>0 se demuestra de forma análoga (hacerlo como ejercicio). c.q.d.

Por tanto para determinar si uno de los ceros de la segunda derivada es un punto de inflexión se calcula la tercera derivada y se evalúa en ese punto, si el resultado es distinto de cero se tiene un punto de inflexión. Si el resultado sale cero tenemos que calcular la cuarta derivada, si al evaluar en ese punto el resultado es distinto de cero no es un punto de inflexión (es un máximo o un mínimo) si sale cero tenemos que calcular la siguiente derivada y reiterar el proceso y así sucesivamente.

PROBLEMA DE LA LATA

maximoy minimo

Crecimiento y decrecimiento.

Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto:

? Una función f(x) es creciente en un punto a, si su derivada es positiva ? Una función f(x) es decreciente en un punto a, si su derivada es negativa. Es decir,

Si Si

Como Þ ,es decir, la función es creciente en

En este caso Þ , es decir, la función es decreciente en

x = a Estudiar la monotonía de una función es hallar los intervalos en los que es creciente y decreciente.

Se procede de la siguiente forma:

• Se halla la derivada, se iguala a cero y se resuelve la ecuación resultante • Con los puntos en los que se anula la derivada dividimos el dominio en intervalos. • Se estudia el signo de la derivada en un punto cualquiera de cada uno de los intervalos resultantes.

Ejemplo 1.

Halla los intervalos de crecimiento y decrecimiento de la función

Hallamos la derivada: La igualamos a cero y resolvemos la ecuación resultante:

  Þ  

Dividimos el dominio R por los puntos 3 y 1 y obtenemos los intervalos

 ,     y    

Estudiamos el signo de la derivada en un punto cualquiera de cada intervalo: Para x = 0, , es decir, positiva Para x = 2, , es decir, negativa Para x = 4, , positiva

La monotonía de la función queda reflejada en la siguiente tabla: Intervalos (- ∞, 1) (1, 3) (3, +∞) Signo de la derivada + - + Función Þ à Þ

Máximos y mínimos. Son los puntos en que la función cambia de monotonía.

? Si una función derivable presenta un máximo o un mínimo en un punto , entonces

En el punto de abscisa x = c la función pasa de creciente a decreciente

Geométricamente significa que la tangente en el punto x = c es horizontal ? Si y existe la segunda derivada, se verifica:

     Si  , hay un mínimo relativo en el punto c

     Si  , hay un máximo en dicho punto.

Demostración: Lo hacemos para el caso de mínimo: Si la función es creciente en c luego

 Y como  ,   , es decir, la derivada es negativa a la izquierda de c (función decreciente) y positiva a la derecha (función creciente), por tanto, existe mínimo relativo en c.

Derivadas

CRITERIOS DE LA PRIMERA DERIVADA

La base del presente criterio radica en observar que los máximos o mínimos locales son consecuencia de observar los siguientes hechos:

 

1.- Cuando la derivada es positiva la función crece.

2.- Cuando la derivada es negativa la función decrece.

3.- Cuando la derivada es cero la función tiene un máximo o un mínimo.

 

Sea f(x) una función y c un número en su dominio. Supongamos que existe a y b  con a<c<b tales que

 

1.-  f es continua en el intervalo abierto (a,b) (de acuerdo con el teorema de Rolle)

2.- f es derivable en el intervalo abierto (a,b), excepto quizá en c;

3.- f´(x) es positiva para todo x<c en el intervalo y negativa para todo x>c en el intervalo.

 

Entonces f tiene un máximo local en c.

 

Nótese que un criterio similar puede tenerse para obtener un mínimo local, solo es necesario intercambiar  “positivo”  por “negativo”.

 

 

 

De manera intuitiva podemos observar que para determinar si existe un máximo o un mínimo  basta graficar alrededor de los puntos donde se ha presentado un cambio de signo Es también importante tener en consideración que el termino alrededor del cambio de signo de la derivada de la función es muy relativo y es este punto donde tenemos que tener la máxima consideración.

Un punto mas a considerar es el tener en cuenta que solo es necesario considerar no solo el cambio de signos para la derivada Por ejemplo, para el caso de la función:

 

la función entre el intervalo (-1,1) tiene un cambio de signo, sin embargo, la función no es diferenciable en el punto x = 0, pese a eso si existe un mínimo local.

CRITERIOS DE LA SEGUNDA DERIVADA

Uno de los ordenes de derivación es el de la segunda derivada, aunque no es despreciable la utilización de las derivadas de orden superior, sobre todo en cálculo de errores. Curiosamente las aplicaciones físicas implican, por lo general, derivadas de segundo orden como podría ser las ecuaciones de movimiento.

 

En esta sección presentaremos una interpretación gráfica de los criterios de la segunda derivada que nos servirá para poder obtener los máximos o mínimos de una función. Antes de analizar como es la relación de la segunda derivada conoceremos algunas definiciones:

 

Definición.

Cóncava hacia abajo. Se dice que una función es  cóncava  hacia abajo cuando la primera derivada es  creciente en un intervalo abierto (a,b)

 

 

 

Definición.

Puntos de inflexión y número de inflexión. Sea f una función y a un número. Supongamos que existe números b y c tales que b<a<c  y además:

a)      f es una función continua en el intervalo abierto (b,c)

b)      f es una función cóncava hacia arriba y cóncava hacia abajo en (a,c), o viceversa.

 

Bajo las condiciones anteriores el punto (a,f(a)) se llama punto de inflexión, y al número a se llama número de inflexión.

 

Si la segunda derivada f´´ de una función f es positiva en un intervalo abierto (a,b) es porque la primera derivada f´ es creciente en ese  intervalo.

 

 

 

 

SEGUNDA PARTE DE DERIVACIÓN

DERIVACIÓN EN CADENA

En cálculo, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones.

DERIVACIÓN IMPLICITA

En los cursos de cálculo la mayor parte de las funciones con que trabajamos están expresadas en forma explícita, como en la ecuación

dónde la variable y está escrita explícitamente como función de x. Sin embargo, muchas funciones, por el contrario, están implícitas en una ecuación. La función y = 1 / x, viene definida implícitamente por la ecuación: x y = 1.

DERIVADAS

Derivada de una función constante

Sea una función constante f(x) = C.

Su gráfica es, como se sabe, una recta paralela al eje de abscisas. Puesto que para cualquier valor de la abscisa su ordenada correspondiente es, constantemente, igual a C, si a es un punto cualquiera del campo de definición de f(x), f(a + h) - f(a) = C - C = 0, por lo que

Luego la derivada de una constante es siempre cero.

            Derivada de la función exponencial
es conocida formalmente como la función real e^x, donde e es el número de Euler, aproximadamente 2.71828.... Esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=e^x ó exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma    

Derivada de un cociente

es un método de encontrar la derivada de una función que es el cociente de dos otras funciones para las cuales existe la derivada.

La función a derivar, f(x), puede escribirse como

Derivada de un  producto

En análisis matemático, la regla del producto o regla de Leibniz para la derivación de un producto, gobierna la derivación del producto de funciones derivables.
Puede declararse informalmente como "la derivada de la primera por la segunda sin derivar más la primera sin derivar por la derivada de la segunda" o matemáticamente:

• 
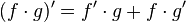
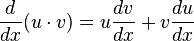• (Notación de Leibniz)

Obviamente al resolverse como una suma de productos, el orden no importa, lo importante es que no se confunda f(x), g(x), f'(x) y g'(x).

Derivada de una raiz

La derivada de la raíz enésima de una función es igual a la derivada del radicando partida por la n veces la raíz enésima de la función radicando elevada a n menos uno.

viernes 8 de octubre de 2010

POSIBLE SOLUCION AL PROBLEMA

DESCRIPCIÓN DEL PROBLEMA

"En este proyecto, se investiga el modo más económico de formar una lata. En primer lugar, esto significa que se da el volumen V de una lata cilíndrica y  necesita hallar la altura h y el radio r que minimice el costo del metal para fabricarla. Si hace caso omiso de cualquier desecho de metal en el proceso de fabricación, el problema es minimizar el área superficial del cilindro. En el ejemplo 2 de la sección 4.7, se resolvió este problema y halló que h=2r; es decir, la altura debe ser igual al diámetro. Pero si usted va a su alacena o al supermercado con una regla, descubrirá que la altura suele ser mayor que el diámetro y que la relación h/r varía desde 2 hasta alrededor de 3.8." 

MALLA

 OBJETIVO DE GRADO:
Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.


PREGUNTA PROBLEMATIZADORA:
¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?


CONCLUSIONES :


°ENTREMOS QUE RESOLVER ALGUNOS PROBLEMAS POR LE METODO CEMENTERIO Y EL METODO ANALITICO


° RESOLVEREMOS ALGUNOS PROBLEMAS DE LA VIDA COTINIANA  QUE INVOLUCREN ,MINIMIZAR   O MAXIMIZAR  CANTIDADES Y COSTOS


° SE ESTABLEZERA UNA PREGUNTA PROBLEMATIZADORA

GRADO:        ONCE PERIODO:    PRIMERO

INTENSIDAD HORARIA :   3 horas semanales DOCENTE:                           GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

Desigualdades e Inecuaciones. Axiomas de orden en R. Intervalos. Propiedades de las desigualdades Problemas. VALOR ABSOLUTO. Definición. Propiedades. Ejercicios FUNCIONES. Definición. Funciones básicas Dominio, Rango Problemas de la vida.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Resolver inecuaciones por  el método del cementerio Y el método analítico. Resolver ecuaciones e inecuación que contienen valores absolutos. Aplicar la definición de función a diferentes relaciones. Resolver problemas que involucran funciones.

Resuelve inecuaciones por  el método del cementerio Y el método analítico. Resuelve ecuaciones e inecuación que contienen valores absolutos. Aplica la definición de función a diferentes Resuelve problemas que involucran funciones.

1. La solución de inecuaciones por  el método del cementerio Y el método analítico. 2. La solución de   ecuaciones e inecuación que contienen valores absolutos. 3.  La aplicación de  la definición de función a diferentes relaciones 4. La solución a problemas que involucran funciones. El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

GRADO:        ONCE PERIODO:     SEGUNDO

INTENSIDAD HORARIA :    3 horas semanales DOCENTE:                            GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

Transformación de funciones. Desplazamientos Verticales. Desplazamiento horizontal. Reflexión. Estiramiento y acortamiento vertical. Acortamiento y alargamiento horizontal. Función par e impar. Dominio, Rango. Interceptos. Función uno a uno Y sobre. Función Inyectiva. Función Inversa.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Graficar funciones partiendo de funciones básicas, empleando los conceptos de traslación, estiramiento, encogimiento y reflexión. Determinar el Dominio, el Rango y los intersectos de una función. Identificar, clasificar una función en par o impar. Identificar si una función tiene inversa y calcularla.

Grafica funciones partiendo de funciones básicas, empleando los conceptos de traslación, estiramiento, encogimiento y reflexión. Determina el Dominio, el Rango y los intersectos de una función. Identifica, clasifica una función en par o impar. Identifica si una función tiene inversa y la calcula

1. La gráfica de una función usando funciones básicas, desplazamientos verticales y horizontales. 2. La gráfica de una función usando funciones básicas, alargamientos y reflexiones verticales y horizontales 3. El cálculo del Dominio, Rango, Interceptos. 4. La determinación si la gráfica de una FUNCIÓN es inyectiva y, si por lo tanto tiene Inversa. . El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

RECURSOS PEDAGOGICOS Ordenadores, programas o proyectos virtuales como DESCARTES y GEOGEBRA, DVD’, sala de informática, Internet, libros virtuales, papel cuadriculado, lápiz, reglas, escuadras, libros , fotocopias, borradores, tizas, marcadores, GRUPO GALOIS.

GRADO:        ONCE PERIODO:     TERCERO

INTENSIDAD HORARIA :    3 horas semanales DOCENTE:                            GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

LIMITES. Definición, ejemplos, ejercicios Continuidad, Teorema del valor intermedio. DERIVADA. Recta tangente y normal a una curva. Velocidad instantánea. Definición de Derivada. Reglas de derivación. Regla de la cadena Derivada implícita.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Calcular límites cuando la variable tiende a un valor finito. Eliminar indeterminaciones de la forma 0/0. Determinar la continuidad de una función. Calcular la derivada de funciones.

Calcula límites cuando la variable tiende a un valor finito. Elimina indeterminaciones de la forma 0/0. Determina la continuidad de una función. Calcula la derivada de funciones.

1. El cálculo de límites cuando la variable tiende a un valor finito. 2. La eliminación de indeterminaciones de la forma 0/0. 3. La determinación de la continuidad o no de una función. 4. El calcular la derivada de una función real. . El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

RECURSOS PEDAGOGICOS Ordenadores, programas o proyectos virtuales como DESCARTES y GEOGEBRA, DVD’, sala de informática, Internet, libros virtuales, papel cuadriculado, lápiz, reglas, escuadras, libros , fotocopias, borradores, tizas, marcadores, GRUPO GALOIS.

GRADO:        ONCE PERIODO:     CUARTO

INTENSIDAD HORARIA :    3 horas semanales DOCENTE:                            GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

APLICACIONES DE LA DERIVADA. Máximos y mínimos relativos y absolutos. Números críticos. Teorema del valor medio y el valor extremo. Criterios de la primera y segunda derivada Concavidad. Problemas de OPTIMIZACIÖN.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Hallar máximos y mínimos relativos y absolutos de una función. Obtener valores críticos de una función. Determinar intervalos de crecimiento y decrecimiento. Determinar concavidad. Resolver problemas de Optimización

Halla máximos y mínimos relativos y absolutos de una función. Obtiene valores críticos de una función. Determina intervalos de crecimiento y decrecimiento. Determina concavidad. Resuelve problemas de Optimización

1. Los máximos y mínimos relativos y absolutos de una función. 2. Los valores críticos de una función. 3. Los intervalos de crecimiento y decrecimiento. La Determinación de la concavidad. 4. La solución de problemas de Optimización El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

RECURSOS PEDAGOGICOS Ordenadores, programas o proyectos virtuales como DESCARTES y GEOGEBRA, DVD’, sala de informática, Internet, libros virtuales, papel cuadriculado, lápiz, reglas, escuadras, libros , fotocopias, borradores, tizas, marcadores, GRUPO GALOIS.